Снова о диполе
Начинал когда-то я его рассматривать на примере магнита и его полюсов, вспоминая школьный опыт на уроке физики:

И вскоре я понял, что одинаковые полюса характеризуют диполь двоизма, и что они не отталкиваются, а притягиваются (в парадигме линейности) всего одной силовой линией из их множества, и назвал его "собачьей косточкой" или "гантелькой" (а остальные, выйдя из каждого полюса, тут же на него замыкаются, и потому полюса и не отталкивают друг друга, а друг другу "мешают").
А диполь троизма я назвал "яблочком", ибо его полюса соединены всеми возможными силовыми линиями кроме одной, и если е добавить, то он "схлопнется" в диполь четверизма точка в сфере" через промежуточный диполь "точка в кольце", полюса которого - точка и кольцо - "абстрагируются" от среды, частью которой они были в диполе троизма, и потому становятся её управляющими (а в диполе четверизма полюса себе присваивают свойства среды, оставляя её "пустой" (в промежуточном диполе "пусто" лишь его кольцевое сопло", и он работает в режиме пылесоса, роль сетки, на которой осаждается пыль, которого играют его полюса, "прирастающие" в процессе его работы не массой, а степенью своей плотности- то есть своей удельной массой, и когда она становится максимально возможной, промежуточный диполь и "схлопывается" в диполь четверизма)).
И теперь о физике диполей, берущейся из физики сред, которую раньше не описывал...
Диполь двоизма характеризуется резко выраженной "горкой" (градиентом) между полюсами, названной мной улицей с односторонним движением.
Градие́нт (от лат. gradiens, род. п. gradientis «шагающий, растущий») — вектор, своим направлением указывающий направление наибольшего возрастания некоторой скалярной величины φ, значение которой меняется от одной точки пространства к другой, образуя скалярное поле, а по величине (модулю) равный скорости роста этой величины в этом направлении.
И отчего же она возникает?
От качества среды, от сильной её разряжённости, при которой обратная связь полюсов ("отдача") намного слабее прямой.
И в диполе троизма "горка" тоже присутствует, но она гораздо более полога, чем в диполе двоизма.
И если рассмотреть шкалу плотности среды в упрощённом дискретном и ступенчатом её представлении, то диполь двоизма будет первой её ступенью, а диполь троизма последней.
И соответственно, нижним пределом этой шкалы будет "абсолютное ничто (небытие)", а верхним - "абсолютное нечто (бытие)".
И первое сравнимо с паром ("пустыми" (бессодержательными) промежутками между "живыми" мгновениями), а второе со льдом (наполненным содержанием текущим мгновением, вечностью).
(если помните, я в последнее время именно с водой и льдом сравнивал время и мгновение, а теперь, как видите, добавил пар)
И давно хотел заметить, что синусоида, которой я часто пользовался, сильно упрощённо передаёт волновой процесс в разрезе, ибо изображает она границу сред, например, воздушной и водной:
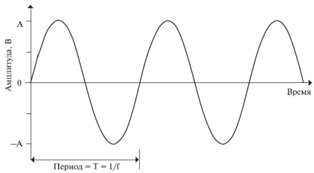
В то время, как "в толще среды" волна не имеет "высоты", и соответственно, ложбины и гребня, ибо, если взять её точку, то мы увидим что она движется по прямой возвратно-поступательным образом, при котором возвратный путь её движения (обратная связь полюсов) короче прямого вследствие сопротивления среды, по причине чего в конце концов волна и сходит на нет.
И кстати, из этого нехитрого наблюдения следует, что выдуманный "великим Эйнштейном" фотон должен двигаться двунаправленно - возвратно-поступательным образом подобно поршню, а не однонаправленно подобно стреле.
И потому Эйнштейну следует очередное "слышал он звон, да не прознал, откуда он".
А двойки по физике он не заслужил, ибо на физику он никогда и не замахивался, ограничиваясь своим бредовым - уменьшением размера тела в направлении его движения, возрастанием его массы вкупе с уменьшением скорости движения "его времени" - при приближении его скорости в скорости света.

